A reader wrote to me and asked the following question about sampling plans by attributes:
What is the “Confidence Level” when using the AQL Tables?
How can we determine what the confidence levels are, and are there formulas we can use?
That’s a valid question. When playing with statistics, one often mentions a confidence interval. For example, “90% of the time, the value will be between 34.5 and 66.0”.
In theory, I guess one could do the same with the values in the AQL tables. There is a formula (but I don’t know anybody who would want to play with a hypergeometric distribution — that’s seriously complicated maths).
However, the statisticians who developed MIL STD 105 (which later became ISO 2859-1, ASQ-ANSI Z1.4, etc.) approached it from another angle and suggested we think about it differently.
The ISO 2859-1 standard comes with a number of operating characteristic curves — the visual representations of that distribution.
And these curves (and the underlying formulae) are based on certain risk levels.
I explained it in the video below:
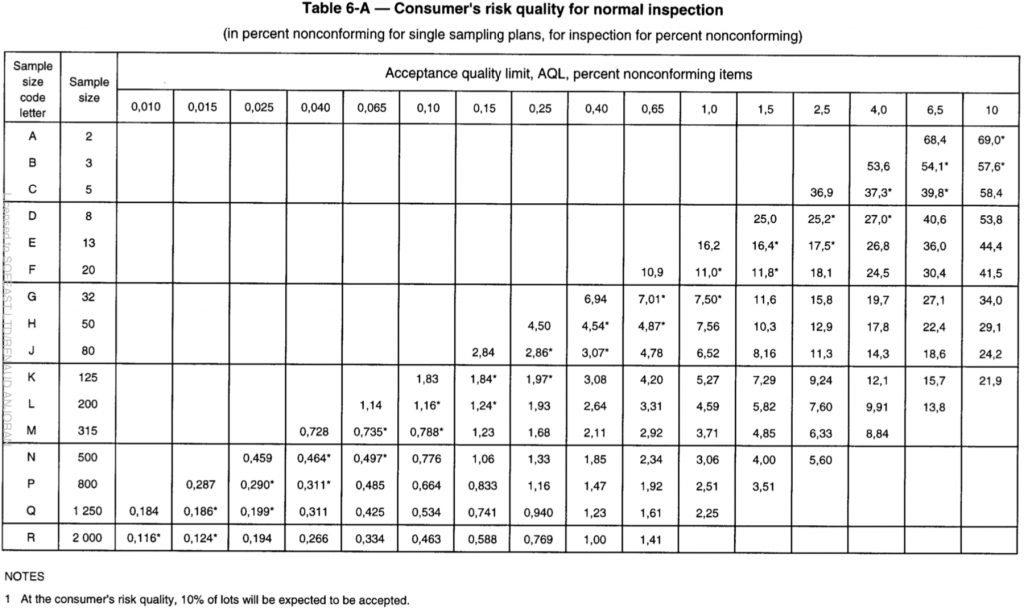
It is also explained in the standard itself. There are tables showing the consumer’s risk and the producer’s risk in different situations.
Let’s look at the risk for the buyer’s side:
EXAMPLE Assume a consumer’s risk quality of 5 % nonconforming items with an associated probability of acceptance of 10 % or less is desired for individual lots. If an AQL of 1 % nonconforming items is designated for inspection of the series of lots, Table 6-A indicates that the minimum sample size shall be given by sample size code letter L.
In practice, I never saw anybody look at these tables. But that’s the risk for the buyer side. If the risk is 5%, the confidence level is 95%.
—
I hope that was clear. Comments and questions welcome!
Get quick results from our AQL calculator!
If you’re performing random quality inspections we have devised a free online AQL calculator which you can use to quickly find your ideal sample size for your quality inspector to pick and also the tolerable major and minor defects.
>> Go to the AQL calculator <<